Алгебра 9 класс учебник Макарычев, Миндюк ответы – номер 583

Учебник по алгебре 9 класс. Авторы: Макарычев, Миндюк, Нешков.

Тип: ГДЗ, Решебник.
Авторы: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И.
Часть: без частей.
Год: 2023-2025.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Екатерина Шамрай

Номер 583.

Укажите наибольшее число членов арифмитической прогресии 3, 5, 7, ... , сумма которых не превосходит 120.

Ответ:

S_n ≤ 120
x₁ = 3
x₂ = 5
d = 5 – 3 = 2

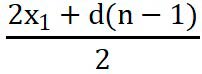S_n = · n

2 · 3 + 2(n – 1)/2 · n ≤ 120

(6 + 2n – 1) · n ≤ 240
4n + 2n² – 240 ≤ 0
n² + 2n – 120 ≥ 0
y = n² + 2n – 120 – парабола, ветви вверх
n² + 2n – 120 = 0
D = 1¹ – 1 · (–120) = 121 = 11²

х = $$\frac{-1 ± \sqrt{121}}{1}$$ = –1 ± 11

n₁ = 10; n₂ = –12 – не является натуральным числом

Ответ: 10 членов прогрессии