Алгебра 8 класс учебник Макарычев, Миндюк ответы – номер 572
- Тип: ГДЗ, Решебник.
- Авторы: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И.
- Часть: без частей.
- Год: 2019-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 572.
.jpg "Изображение решения по алгебре 8 класс Макарычев, Миндюк, Нешков, Суворова номер 572")
Номер 572.
От прямоугольного листа картона, длина которого равна 60 см, а ширина - 40 см, отрезали по углам равные квадраты и из оставшейся части склеили открытую коробку. Найдите сторону квадрата, если известно, что площадь основания коробки равна 800 см².
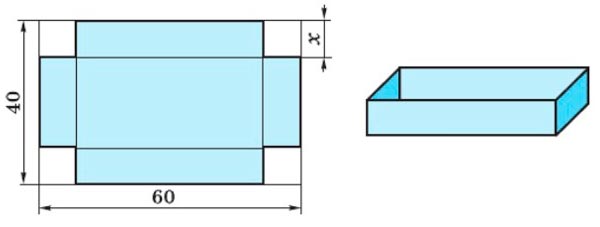
Пусть х − сторона квадрата, тогда х² − площадь одного квадрата, 4х² площадь четырех квадратов. Площадь больших сторон коробки равна (60 − 2х) ⋅ х ⋅ 2, площадь меньших сторон коробки равна (40 - 2х) ⋅ х ⋅ 2. Площадь листа картона равна 60 ⋅ 40 = 2400 см², а площадь основания коробки 800 см². Составим уравнение:
4х² + (60 - 2х) ⋅ х ⋅ 2 + (40 - 2х) ⋅ х ⋅ 2 + 800 = 2400
4х² + 120х - 4х² + 80х - 4х2 + 800 - 2400 = 0
-4х² + 200х - 1600 = 0 : (-4)
х² - 50х + 400 = 0
x₁ = $$
\frac{-b+\sqrt{D}}{2 a}=\frac{50+\sqrt{900}}{2 ⋅ 1}
$$ = 50 + 30/2 = 80/2 = 40
x₂ = $$
\frac{-b-\sqrt{D}}{2 a}=\frac{50-\sqrt{900}}{2 ⋅ 1}
$$ = 50 - 30/2 = 20/2 = 10
х = 40 не подходит, так как ширина листа 40 см, тогда сторона квадрата равна 10 см.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.