Алгебра 8 класс учебник Макарычев, Миндюк ответы – номер 38

Учебник по алгебре 8 класс. Авторы: Макарычев, Миндюк, Нешков.

Тип: ГДЗ, Решебник.
Авторы: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И.
Часть: без частей.
Год: 2019-2024.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Екатерина Шамрай

Отличается задание? Переключите год учебника.

2019 2024

Номер 38.

Постройте график функции
1) Обсудите, что общего у дробей, задающих функцию в заданиях а) и б). Как надо учитывать эту особенность при построении графиков?
2) Распределите, кто выполняет задание а), а кто − задание б), и выполните их.
3) Проверьте друг у друга, правильно ли выполнено задание. Исправьте замеченные ошибки.

а) y = х² − 25/2x + 10
б) y = х³ − 9x/х² − 9

Ответ:

а) область определения функции      2х + 10 ≠ 0      2х ≠ −10      x ≠ −10 : 2      x ≠ −5      Преобразуем функцию
     y = х² − 25/2x + 10 = (х − 5)(x + 5)/2(x + 5) = (х − 5)(x + 5) : (x + 5)/2(x + 5) : (x + 5) = х − 5/2
     y = x − 5/2
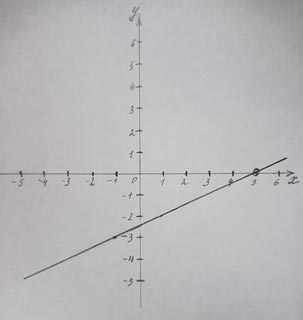
     Построим график функции y = x − 5/2
     $$ \begin{array}{|l|l|l|} \hline x & 1 & -1 \\ \hline y & -2 & -3 \\ \hline \end{array} $$
     x = 1, y = 1 − 5/2 = −4/2 = −2      x = −1, y = −1 − 5/2 = −6/2 = −3
     Исключим на графике точку x = −5

Алгебра 8 класс учебник Макарычев, Миндюк номер 38

б) область определения функции      x² − 9 ≠ 0      x² − 3² ≠ 0      (x − 3)(x + 3) ≠ 0      x ≠ −3, x ≠ 3
     Преобразуем функцию
     y = х³ − 9x/х² − 9 = x(х² − 9)/(х² − 3²) = x(х² − 3²) : (х² − 3²)/(х² − 3²) : (х² − 3²) = x/1 = x
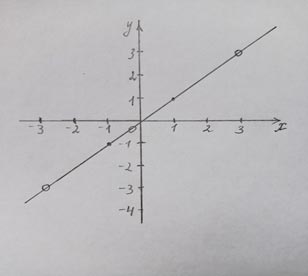
     y = x      Построим график функции y = x
     $$ \begin{array}{|l|l|l|} \hline x & 1 & -1 \\ \hline y & 1 & -1 \\ \hline \end{array} $$
     x = 1, y = 1      x = −1, y = −1      Исключим на графике точки x = −3; 3.