Алгебра 8 класс учебник Макарычев, Миндюк ответы – номер 205
- Тип: ГДЗ, Решебник.
- Авторы: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И.
- Часть: без частей.
- Год: 2019-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 205.
.jpg "Изображение решения по алгебре 8 класс Макарычев, Миндюк, Нешков, Суворова номер 205")
Номер 205.
Зная, что m − целое число, найдите целые значения дроби:
а) m² − 6m + 10/m − 3
б) (m − 4)²/m − 2
1) Обсудите, какие преобразования надо выполнить, чтобы найти целые значения дроби.
2) Распределите, кто выполняет задание а), а кто - задание б), и выполните их.
3) Проверьте друг у друга, правильно ли выполнены преобразования и верно ли найдены целые значения дроби. Исправьте замеченные ошибки.
а) Разделим числитель на знаменатель уголком методом Горнера
m² − 6m + 10 = (m − 3)(m − 3) + 1 = (m − 3)² + 1
m² − 6m + 10/m − 3 = (m − 3)² + 1/m − 3 = (m − 3)²/m − 3 + 1/m − 3 = (m − 3)(m − 3)/m − 3 + 1/m − 3 = (m − 3)(m − 3) : (m − 3)/(m − 3) : (m − 3) + 1/m − 3 = m − 3/1 + 1/m − 3 = m − 3 + 1/m − 3
Значение выражения m - 3 при любом целом m является целым числом.
Значение выражения 1/m − 3 принимает целые значения при знаменателе равном −1, 1
m − 3 = −1, m = 2
m − 3 = 1, m = 4
б) Разделим числитель на знаменатель уголком методом Горнера
(m − 4)² = m² − 8m + 16
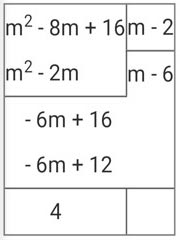
m² − 8m + 16 = (m − 2)(m − 6) + 4
(m − 4)²/m − 2 = m² − 8m + 16/m − 2 = (m − 2)(m − 6) + 4/m − 2 = (m − 2)(m − 6)/m − 2 + 4/m − 2 = (m − 2)(m − 6) : (m − 2)/(m − 2) : (m − 2) + 4/m − 2 = m − 6/1 + 4/m − 2 = m − 6 + 4/m − 2
Значение выражения 4/m − 2 принимает целые значения при знаменателе равном −4, 4, −2, 2, −1,1
m − 2 = −4, m = −2
m − 2 = 4, m = 6
m − 2 = −2, m = 0
m − 2 = 2, m = 4
m − 2 = −1, m = 1
m − 2 = 1, m = 3
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.