Алгебра 7 класс учебник Макарычев, Миндюк ответы – номер 61
- Тип: ГДЗ, Решебник.
- Авторы: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И.
- Часть: без частей.
- Год: 2019-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 61.
Верно ли неравенство:
а) x ≤ 5,3 при x = 2,7; 5,3; 6;
б) y ≥ 4,8 при y = 3,5; 4,8; 7,1;
в) 0,6 < x ≤ 0,8 при х = 0,5; 0,6; 0,7; 0,8; 0,9;
г) 2,1 ≤ y ≤ 2,4 при y = 2,1; 2,2; 2,3; 2,4; 2,5?
.jpg "Изображение решения по алгебре 7 класс Макарычев, Миндюк, Нешков, Суворова номер 61")
Номер 61.
(Для работы в парах.) Докажите, что всякое простое число, начиная с 5, либо увеличинное, либо уменьшенное на 1, делится на 6.
1) Проверьте утверждение на примерах. Одному учащемуся рекомендуем взять простые числа из третьего десятка, другому – из седьмого десятка.
2) Обсудите друг с другом, из чего следует справедливость указанного свойства.
3) Проведите доказательство.
1)
1 ученик
Числа 23, 29
23 – 1 = 22 – не делится на 6
23 + 1 = 24 – делится на 6
29 – 1 = 28 – не делится на 6
29 + 1 = 30 – делится на 6
2 ученик
Числа 61, 67
61 – 1 = 60 – делится на 6
61 + 1 = 62 – не делится на 6
67 – 1 = 66 – делится на 6
67 + 1 = 68 - не делится на 6
2) Справедливость равенства следует из того, что само простое число и числа, уменьшенные и увеличенные на 1, являются тремя последовательными натуральными числами. Известно, что хотя бы одно из них обязательно делится на 3 и хотя бы одно из них является четным, то есть делится на 2. Поэтому одно из этих чисел делится на 6.
3)
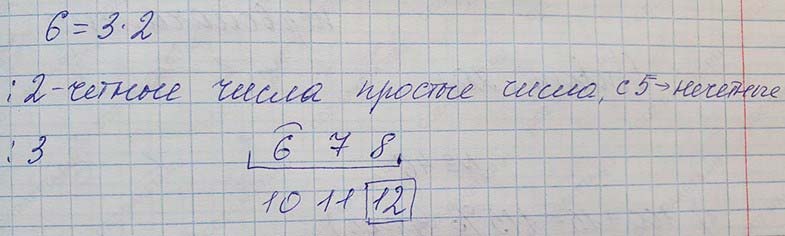
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.